Daniela Remogna

I’ve been a speaker to a London Algorithms Meetup and the subject was Graph Theory.

Here there is the link to the repository: https://github.com/LondonAlgorithms/graph_theory with the javascript code.

I have created a pairing exercise with specs to guide through the creation of an undirect Graph by using an adjacency list. After all the vertices and edges have been added to the Graph, the exercise requires to visit a Graph with a Breadth First Search Algorithm. In the repo I have written some Javascript tests to follow during the code development. You can run tests by opening SpecRunner.html.

In the repo there are two branches: master and solution.
As you might expect, solution branch contains the complete javascript code.

After a brief introduction to what is a Graph and which are the use cases, I’ve explained how to build a graph with an Adjacency List and then I’ve shown which are the Graph Traversal Algorithms: Depth First Search and Breadth First Search.

What is a Graph

Graph is a non linear data structure, it contains a set of points known as nodes (or vertices) and set of linkes known as edges (or Arcs) which connects the vertices.

Graphs are used to represent networks of communication, transportation system, website, maps, social networks, chemistry, games etc.

How to build a Graph

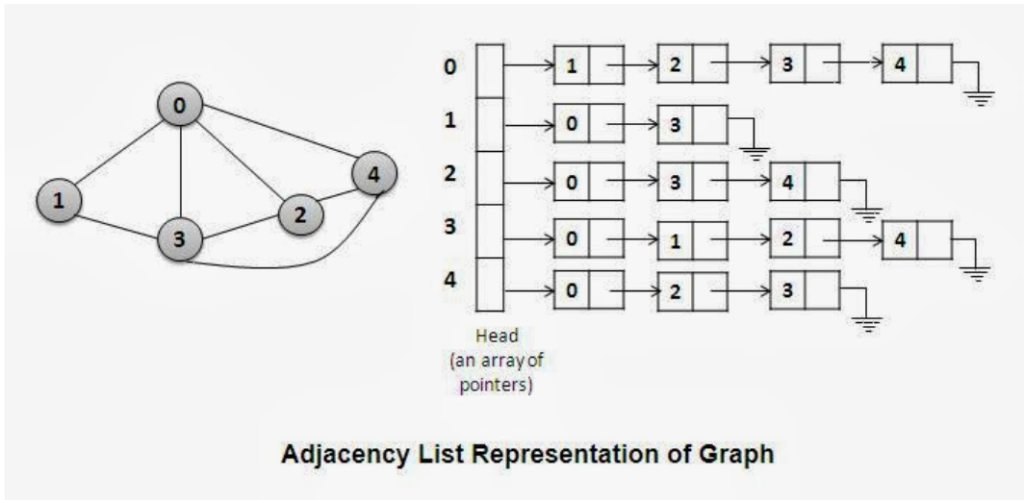
To build a Graph we might use an Adjacency List.

An Adjacency List associates each vertex in the graph with the collection of its neighboring vertices. It uses an hash table to associate each vertex in a graph with an array of adjacent vertices.

How to visit a Graph

There are two search algorithms we can perform on a graph:

1. depth first search (Use a stack – LIFO)
2. breadth first search (Use a queue – FIFO)

Depth-first search involves following a path from the beginning vertex until it reaches the last vertex, then backtracking and following the next path until it reaches the last vertex, and so on until there are no paths left.

There are two ways to visit a Graph with DFS:

1. iterative solution with a stack
2. recursive solution

Keep in mind, any recursive algorithm can be translated to an iterative one by using a stack

Recursive Solution

Unlike trees, graphs may contain cycles, so we may come to the same node again.

To avoid processing a node more than once, we use a boolean wasVisited stored on the Vertex.

DFS-recursive(G, s):
  mark s as visited
  for all neighbours w of s in Graph G:
    if w is not visited:
      DFS-recursive(G, w)

Iterative Solution with a Stack

DFS-iterative (G, s):  //Where G is graph and s is source vertex
  let S be stack
  S.push( s ) //Inserting s in stack 
  while ( S is not empty):
    //Pop a vertex from stack to visit next
    v  =  S.top( )
    S.pop( )
    mark s as visited.
    //Push all the neighbours of v in stack that are not visited   
    for all neighbours w of v in Graph G:
      if w is not visited :
        S.push( w )         

Breath First Search

A breadth-first search moves through a graph layer by layer, first examining layers closer to the first vertex and then moving down to the layers farthest away from the starting vertex.

For breadth first search we don’t use recursion, Breadth-first traversal traditionally uses a queue as helper data structure

Define a queue
Add to queue the starting vertex
Visit the starting vertex
While there is a vertex in the queue
  Get the next vertex to visit from the queue
  Get vertex neighbours 
  For each vertex neighbour
    if the neighbour has not been visited → 
      visit neighbour
      add to the queue

Online BFS algorithm

Link: https://www.cs.usfca.edu/~galles/visualization/BFS.html

I hope you enjoyed this article and happy coding!